JUEGO DE SUMA DE POLINOMIOS.
Con este fantástico juego vas a practicar la suma de polinomios, que te vendrá muy bien para resolver ecuaciones.
JUEGO PARA PRACTICAR LOS PRODUCTOS NOTABLES
JUEGO «CUADRADO DE UNA SUMA».
El cuadrado de una suma de dos sumando es igual al cuadrado del primer sumando más el doble del primero por el segundo más el cuadrado del segundo. (a + b)² = a² + 2ab + b²JUEGO «CUADRADO DE UNA DIFERENCIA».
El cuadrado de una diferencia es igual al cuadrado del primer sumando menos el doble del primero por el segundo más el cuadrado del segundo. (a – b)² = a² – 2ab + b²
JUEGO «SUMA POR DIFERENCIA»
La suma de dos monomios por su diferencia es igual a la diferencia de sus cuadrados.
(a + b) · (a – b) = a² – b²
Aquí os dejo ejercicios resueltos de expresiones algebraicas. 😉
 JUEGO EXPRESIONES ALGEBRAICAS
JUEGO EXPRESIONES ALGEBRAICAS
Diviértete jugando al famoso programa de TV, pero todo relacionado con él álgebra.
JUEGO DE DESCOMPOSICIÓN POLINÓMICA.
Maravilloso juego en el que descomponemos un número como una suma de sus diversos órdenes de unidades.
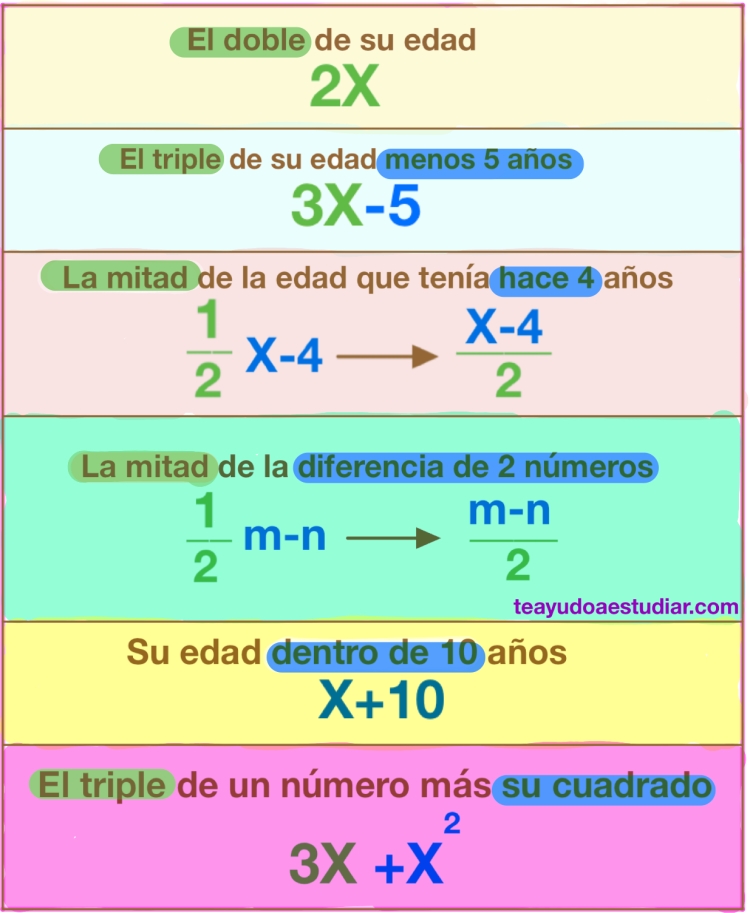
EXPRESIONES ALGEBRAICAS
- El doble de un número 2x
- El triple de un número 3x
- La mitad de un número x/2
- Un tercio de un número x/3
- Un cuarto de un número x/4
- Un número al cuadrado x elevado a dos
- Un número al cubo x elevada a tres
- Dos números consecutivos x y x+1
- Dos números consecutivos pares 2x y 2x+2
- Dos números consecutivos impares 2x+1 y 2x+3
- La suma de dos números es 24 x y 24-x
- El producto de dos números es 24 x y 24/x
- La división de dos números es 24 x y 24 por x
MULTIPLICACIÓN DE NÚMEROS ENTEROS
+ × + = + → 5 × 3 = 15 POSITIVO
−× − = + → −5×(−3)= 15 POSITIVO
+ × − = − → 5×(−3)= −15 NEGATIVO
−× + = − → −5×(−3)= −15 NEGATIVO
DIVISIÓN DE NÚMEROS ENTEROS
+ : + = + → 6 : 3 = 2 POSITIVO
−: − = + → −6:(−3)= 2 POSITIVO
+ : − = − → 6 :(−3)=−2 NEGATIVO
−: + = − → −6: 3 = −2 NEGATIVO
SUMA DE NÚMEROS ENTEROS
Si los signos son iguales, se suma y se mantiene el signo:
+ + + = + → 6 + 6 = 12 POSITIVO
− + − = − → -6+(-6)=-12 NEGATIVO
Si los signos son diferentes, se resta y se pone el signo del número que tenga el mayor valor absoluto:
6 + (-3) = 3 POSITIVO porque el número 6 es más grande que el 3 y se pone su signo.
-6 + 3 = -3 NEGATIVO porque el número 6 es más grande que el 3 y se pone su signo.
RESTA DE NÚMEROS ENTEROS
El símbolo de la resta le cambia el signo a la cifra que le sigue y la resta pasa a ser una suma, es decir, el -3 pasa a ser +3 y la resta pasa a ser una suma.
6 – (-3) = 6 + (+3) = 9 POSITIVO
POTENCIA DE NÚMEROS ENTEROS
(+) elevado a par= +
(-) elevado a par = +
(+) elevado a impar = +
(-) elevado a impar = –
- La potencia de 0 es 1.
a0 =1
(− a)0 =1
- La potencia con exponente negativo es su inversa positiva.
- Producto con la misma base → se mantiene la base y se suman los exponentes.
4².4³ = 4²+³
- División con la misma base → se mantiene la base y se restan los exponentes.
4³ : 4² = 4³¯² = 4
- Potencia de una potencia → se mantiene la base y se multiplican los exponentes.
(4³)² = 4³·²
- Producto con diferentes bases y mismos exponentes → se multiplican las bases y se mantiene el exponente.
23 · 43 = (2 · 4)3=83
- División con diferentes bases y mismos exponentes → se dividen las bases y se mantiene el exponente.
63 : 33 = (6:3)3 = 23
Pasos para resolver ecuaciones
Una ecuación está formada por dos miembros, el primer miembro es todo lo que hay delante del igual y el segundo miembro es todo lo que hay detrás del igual. Y por términos, que son cada uno de los sumandos que forman la ecuación.
- Quitar paréntesis.
- Quitar denominadores.
- Agrupar los términos con x en un miembro y los independientes en el otro miembro.
- Reducir los término semejantes.
- Despejar la incógnita.
Ejemplo:

El menos que hay delante del paréntesis hace que cambie de signo todo lo que hay dentro del paréntesis. Y así puedo quitar el paréntesis.

Calculo el denominador común (con el m.c.m.) y así puedo quitar denominadores que en este caso es 12.

Quito el primer paréntesis: el 6 multiplica a la x dando 6x y luego al -3 dando -18. Quito el segundo paréntesis: el menos cambia de signo a todo el 5x pasa a ser -5x y el -3 pasa a ser +3.

Agrupamos términos poniendo todos los términos que tienen x en el primer miembro y todos los que no tienen x en el segundo miembro.

Sumamos términos.

Despejamos la incógnita pasando el -9 que está multiplicando a la x, lo pasamos al otro lado dividiendo y hacemos la división de :
-27/-9 = 3
